最近疫情在家没法出门,因此尝试去找找工作,投递了一些大厂的职位,也有一些好心猎头帮我推荐。但是实在是不好意思,一面都过不了。 不过我似乎也没有太大期待了。毕竟这玩意对于我来说,还是看运气啦,只是纯当找个人说说话,顺便还能聊聊看自己如果找工作还有哪些不足。
其中腾讯音乐前天打电话面试,最后问了我一个算法问题,四个砝码可以称出多少种重量。
我当时听到砝码这两个字竟然没有反应过来,还问了下砝码是什么,天平上那个吗?感觉几百年没有听到过这个词了,有点懵逼。面试的让我说思路,我想这不就是一个数学题吗?排列组合想了一下,但转念一想 他没告诉我重量,我怎么知道可以称出多少种重量呢? 比如 2,4,6,8 可以用2和4 称出6,也可以用一个6 称出6 呀。那这算一种吗?好像还不对,我还可以用 一个2 称出一个二,用一个4,和6 ,把物品放在4的那一边称出一个二的重量来呀。我靠,这事情太复杂了。然后就乱了。最后挂断电话,面试结束。
后来我想了想C44+C43+C42+C41 =15 呀,这还要什么思路吗? 想起他说的是算法?这tm是让我说算法吧。这不就是找出一个数组中有多少个子数组吗。至于放到两边的做法应该是不需要考虑吧。
所以问题简化为求的一个数组中子数组的组合方式有多少。
我晚上花了一些时间写了一下。采用的是动态规划的方式。
import java.util.*;
//给定若干个砝码,求起能够称出多少种重量
public class WeightSolution {
private List<int[]> getSubArray(int[] weights) {
List<int[]> result = new LinkedList<>();
for (int i = 1; i <= weights.length; i++) {
result.addAll(getSubBySize(i, weights));
}
return result;
}
private List<int[]> getSubBySize(int size, int[] weights) {
List<int[]> result = new LinkedList<>();
List<int[]> found = find(size, weights, 0, weights.length);
for (int[] ints : found) {
int[] values = new int[ints.length];
for (int i = 0; i < ints.length; i++) {
values[i] = weights[ints[i]];
}
result.add(values);
}
return result;
}
//返回数组的下标的数组
private List<int[]> find(int size, int[] weights, int start, int end) {
List<int[]> result = new LinkedList<>();
if (size == 1) {
for (int i = start; i < end; i++) {
result.add(new int[]{i});
}
return result;
}
List<int[]> cached = new LinkedList<>();
List<int[]> rs = find(size - 1, weights, 0, weights.length);
for (int i = 0; i < weights.length; i++) {
int first = i;
for (int[] r : rs) {
if (notIn(first, r)) {
int[] newS = new int[r.length + 1];
newS[0] = first;
System.arraycopy(r, 0, newS, 1, r.length);
if (!isExist(newS, cached)) {
result.add(newS);
cached.add(newS);
} else {
// System.out.println("已存在:" + changeToStr(newS));
}
}
//去重
}
}
return result;
}
//是否存在缓存中
private boolean isExist(int[] r, List<int[]> ls) {
for (int[] s : ls) {
if (s.length != r.length) {
continue;
}
int[][] matrix = new int[s.length][s.length];
int[] a = r;
int[] b = s;
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
matrix[i][j] = (a[i] == b[j] ? 1 : 0);
}
}
boolean isEqual = true;
for (int i = 0; i < matrix.length; i++) {
int countH = 0;
for (int j = 0; j < matrix[i].length; j++) {
if (matrix[i][j] == 1) {
countH++;
int countV = 0;
for (int k = i; k < matrix.length; k++) {
if (matrix[k][j] == 1) {
countV++;
}
}
if (countV != 1) {
isEqual = false;
break;
}
}
}
if (countH != 1) {
isEqual = false;
break;
}
}
if (isEqual) {
return true;
}
}
return false;
}
private boolean notIn(int a, int[] ls) {
boolean in = true;
for (int l : ls) {
if (a == l) {
return !in;
}
}
return in;
}
public static void main(String[] args) {
int[] rs = new int[]{1, 2, 5, 10};
// print(new WeightSolution().getSubBySize(2, rs));
print(new WeightSolution().getSubArray(rs));
}
public static void print(List<int[]> list) {
for (int[] ints : list) {
System.out.print(Arrays.toString(ints));
int sum = 0;
for (int anInt : ints) {
sum += anInt;
}
System.out.print("->" + sum + ";");
}
System.out.println("WeightSolution.print");
System.out.println("称重方法有 [" + list.size() + "]");
}
}
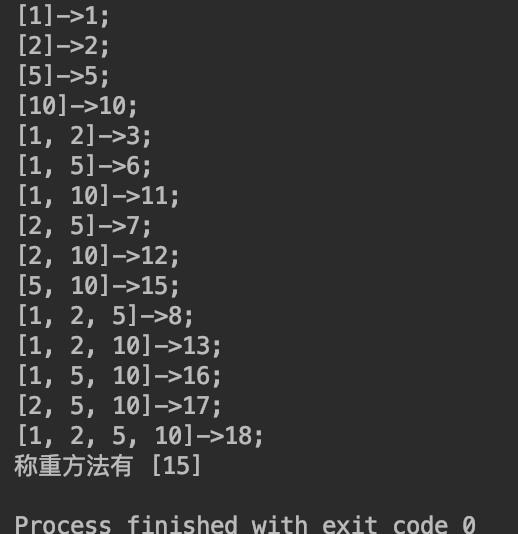
核心思想是,用数组角标形成的数组代表dp的解,如果有N个元素的数组S,
以1为长度子元素解为:
dp(1)={[0],[1],…[n-1]}
以2 为长度的解为:
Si*dp(1) where Si not in dp(1),
以此类推,
dp(n)=dp(n-1)*Si where Si not in dp(n-1) , i=0…n
这样就构成了一个状态转移方程。
我的程序是自顶向下求的解,当然还有很多优化空间。没有做缓存,当数组长度增加,计算量也呈现指数增加。
如果需要考虑放置天平两边,则需要在从得到的解集合中抽出任意两组没有公共元素的集合,再计算各自总和的差值,即可得到更加多的称重方法。
